martes, 31 de mayo de 2011

4.1 Definición de serie

En matemáticas, una serie es la suma de los términos de una sucesión.
Se representa una serie con términos an como
Siendo N es el índice final de la serie.

Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales.
Las series convergen o divergen.
Una serie diverge      si

No existe o si tiende a infinito;
Converge si:

Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir,  .
Las series convergen o divergen. En cálculo, una serie diverge si   no existe o si tiende a infinito; puede converger si   para algún  .
Serie finita
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de Cauchy de   y   se verifica es  . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
Serie infinita
Primer ejemplo. Para alguna  , sea   y  . Entonces

por definición y la fórmula binomial. Dado que, formalmente,   y  , se ha demostrado que  . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series (véase debajo), se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo  .
Segundo ejemplo. Sea x(n) = 1 para todo  . Entonces C(x,x)(n) = n + 1 para todo   por lo tanto el producto de Cauchy   y no es convergente.
Publicado por en No hay comentarios:

Evaluacion Parcial

Por medio de la presente informo que el equipo obtuvo el 93% de los 6 subtemas publicados.

Atte.
Ing.Jose Enrique Marquez Eloiza
Publicado por en No hay comentarios:

lunes, 30 de mayo de 2011

4.2 SERIE NUMERICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (criterio de D´Alembert) y PRUEBA DE LA RAÍZ (criterio de Cauchy).

SERIE NUMERICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (criterio de D´Alembert) y PRUEBA DE LA RAÍZ (criterio de Cauchy).


Imaginemos que se va a celebrar una carrera con las siguientes reglas:


1. El primer minuto debe recorrerse 100 metros.


2. El minuto siguiente debe recorrerse la mitad, 50 metros.


3. El minuto siguiente debe recorrerse la mitad del anterior, 25 metros.


4. El minuto siguiente dee recorrerse la mitad del anterior, 12,50 metros.
y as´ı sucesivamente.


Por otra parte, al mismo tiempo empieza otra carrera, con las reglas ligeramente
modificadas:


1. El primer minuto se recorren 100 metros.


2. El minuto siguiente se recorren la mitad de 100 metros, 50 metros.


3. El minuto siguiente se recorren la tercera parte de 100 metros, 33,3
metros.


4. El minuto siguiente se recorren la cuarta parte de 100 metros, 25 metros.
y as´ı sucesivamente.


Dos corredores empiezan a la vez las carreras. Si la meta de la primera se
encuentra situada a 300 metros y la de la segunda a 1000 metros, ¿qui´en
llega primero a la meta y cu´anto tiempo tarda?
Llamamos D = 100 metros la distancia recorrida en el primer minuto. La
primera carrera va recorriendo las distancias:


D +D/2+D/4+D/8+ . . .


La segunda carrera va recorriendo las distancias:


D +D/2+D/3+D/4+ . . .


La pregunta es cu´al de estas sumas alcanza la distancia a la que est´a situada
la meta respectiva. Al acabar este tema deberemos ser capaces de dar una
respuesta razonada1.


Series de Convergencia
Son aplicables en caso de disponer de otra serie \sum(b_n) tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:


Criterio de comparación directa ( de la mayorante o de Gauss )

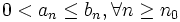
Si 0 < a_n \le b_n , \forall n \ge n_0
  • Si \sum(b_n) converge \Rightarrow \sum(a_n) converge
  • Si \sum(a_n) diverge \Rightarrow \sum(b_n) diverge


Criterio de comparación por paso al límite del cociente

\lim_{k \rightarrow \infty} \left ( \frac {a_{k}}{b_k} \right )=L
Entonces:
  • Si L = 0 y \sum(b_k) converge \Rightarrow \sum(a_k) converge
  • Si L=\infty y \sum(b_k) diverge \Rightarrow \sum(a_k) diverge
  • En otro caso, ambas series comparten la misma condición (ambas convergen, o bien ambas son divergentes).


CONVERGENCIA
Una serie alternada an converge absolutamente si
\sum_{n=1}^\infty \left| {a_n}\right|
es una serie convergente. Se demuestra que una serie que converge absolutamente, es una serie convergente.


Criterio de D'Alembert 
Sea una serie \sum_{k=1}^{\infty} a_k, tal que ak > 0 ( serie de términos positivos).
Si existe
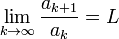
\lim_{k \rightarrow \infty} \frac {a_{k+1}}{a_k}=L
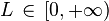con L \, \in \, [0, +\infty), el Criterio de D'Alembert establece que:
  • si L < 1, la serie converge.
  • si L > 1, entonces la serie diverge.
  • si L = 1, no es posible decir algo sobre el comportamiento de la serie.
En este caso, es necesario probar otro criterio, como el criterio de Raabe


Criterio  de Cauchy



Si f(x) es una función positiva y monótonamente decreciente definida en el intervalo [1, ∞) tal que f(n) = an para todo n, entonces \textstyle \sum{a_n}converge si y sólo si \textstyle \int_1^\infty f(x)\,dx  es finita.
Más generalmente, y para el tipo de función definida antes, pero en un intervalo [N,∞), la serie
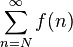
\sum_{n=N}^\infty f(n)
converge si y sólo si la integral
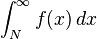
\int_N^\infty f(x)\,dx
converge
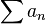Sea \sum{a_n} una serie monótona de números positivos decrecientes. \sum_{n=1}^\infty {a_n} converge si y sólo si la serie
\sum_{n=1}^\infty {2^na_{2^n}} converge

BIBLIOGRAFIA:
http://es.wikipedia.org/wiki/Serie_matemática#Criterio_de_D.27Alembert_o_Criterio_del_Cociente_.28Criterio_de_la_raz.C3.B3n.29
MC. Marcel Ruiz Martínez


Publicado por en No hay comentarios:

jueves, 26 de mayo de 2011

Evaluacion parcial

El equipo obtuvo el 99% de la realizacion del trabajo.
Publicado por en No hay comentarios:

4.3 Serie de potencias

Series de potencias. Desarrollos en serie
de Taylor
En la representación (e incluso en la construcción) de funciones, desempeñan un papel especialmente
destacado cierto tipo de series, denominadas series de potencias. Los aspectos profundos de su
estudio corresponden a la teoría de funciones de variable compleja más que a la teoría de funciones
de variable real, por lo que aquí damos simplemente algunas propiedades sencillas, suficientes para
nuestros propósitos.Series de potencias. Convergencia de las series de potencias. Recibe el nombre de serie de potencias toda serie de la forma ∞Σ n=0 an(x−c)n.
El número real an se denomina coeficiente n-ésimo de la serie de potencias (obsérvese que el término
n-ésimo de la serie es an(x−c)n). Si los coeficientes a0, a1, am−1 son nulos, la serie suele escribirse ∞Σ n=m an(x−c)n.
En cierto modo, se trata de una especie de polinomio con infinitos términos. Vamos a ver que   las funciones definidas como suma de una serie de potencias comparten muchas propiedades con los
polinomios.
¿Para qué valores de x converge una serie de potencias? Obviamente, es segura la convergencia para x =c, con suma a0, y puede suceder que éste sea el único punto en el que la serie converge. Fuera de este caso extremo, la situación es bastante satisfactoria: veamos algunos ejemplos.
Ejemplos. a) La serie geométrica ∞Σ n=0 xn converge (absolutamente) si y solo si x " (−1,1) (con suma 1 1−x , como sabemos). 
b) La serie ∞Σ n=1 xn n converge si y solo si x " [−1,1). Si x " (−1,1), converge absolutamente.
c) La serie ∞Σ n= xn n2 converge (absolutamente) si y solo si x " [−1,1].
d) La serie ∞Σ n=1(−1)nx2nn converge si y solo si x " [−1,1]. Si x " (−1,1), converge absolutamente.
e) La serie∞Σn=0xnn!converge (absolutamente) para todo x " R (y la suma es ex).
f) La serie∞Σn=0n!xn converge solamente para x = 0. Si para algún r " (0,+∞) la sucesión (anrn) está acotada, entonces para cada x " R tal que |x−c| < r la serie ∞Σ n=0 an(x−c)n es absolutamente convergente.


Publicado por en No hay comentarios:

4.4 Radio de convergencia.

Definición 

Si nos limitamos al conjunto de los números reales, una serie de la forma \sum_{n=0} a_n(x-x_0)^n, con a_n,x,x_0\in\mathbb{R}, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. 


Ejemplo:
Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.
[editar] Radio de convergencia finito

La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto:

\frac{1}{1-x}=\sum_{n=0}^\infty x^n=1+x+x^2+x^3+....

(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho

\sum_{n=0}^\infty 0.25^n=1+0.25+0.25^2+0.25^3+...=\frac{4}{3}.

(la cuenta se puede hacer por serie de potencia). Y por otro lado

\frac{1}{1-0.25}=\frac{1}{1-\frac{1}{4}}=\frac{4}{3}.

Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:

\sum_{n=0}^\infty 2^n=1+2+2^2+2^3+...=\infty.
[editar] Distancia a la singularidad

El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x0 = 3 tiene la forma:

\frac{1}{1-x}=-\frac{1}{2}+\frac{x-3}{4}-\frac{(x-3)^2}{8}+\frac{(x-3)^3}{16}-....

Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:

\frac{1}{1+x^2}=\frac{1}{2}-\frac{x-1}{2}+\frac{(x-1)^2}{4}-\frac{(x-1)^4}{8}+\frac{(x-1)^5}{8}-...

Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es r=\sqrt{2}/2. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador. Por ejempo, la función ex puede desarrollarse en series de potencia de x − 0 = x, de hecho e^{x}=\sum_{n=0}^\infty x^n/n!=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+.... y esto vale para todo real x por eso el radio de convergencia será infinito.

Publicado por en No hay comentarios:

4.5

SERIE DE TAYLOR

La serie de Taylor es una serie funcional y surge de una ecuación en la cual se puede encontrar una solución aproximada a una función.

La serie de Taylor proporciona una buena forma de aproximar el valor de una función en un punto en términos del valor de la función y sus derivadas en otro punto.

Por supuesto, para hacer esta aproximación sólo se pueden tomar unas cuantas expresiones de esta serie, por lo que el resto resulta en un error conocido como el término residual, es a criterio del que aplica la serie en numero de términos que ha de incluir la aproximación.

Pueden resolver por aproximación funciones trigonométricas, exponenciales, logarítmicas etc...

La serie de Taylor se basa en ir haciendo operaciones según una ecuación general y mientras mas operaciones tenga la serie mas exacto será el resultado que se esta buscando. Dicha ecuación es la siguiente:

Donde n! es el factorial de n

F(n) es la enésima derivada de f en el punto a

Como se puede observar en la ecuación, hay una parte en la cual hay que desarrollar un binomio (x-a) n por lo que para simplificar el asunto se igualara a "a" siempre a 0. Para fines prácticos no afecta mucho en el resultado si se hacen muchas operaciones en la serie.

Teorema de Taylor: Si la función f y sus primeras n+1 derivadas son continuas en un intervalo que contiene a a y a x, entonces el valor de la función en un punto x está dado por:


La expansión en series de Taylor de n-ésimo orden debe ser exacta para un polinomio de n-ésimo orden.

Para otras funciones continuas diferenciables, como las exponenciales o sinusoidales, no se obtiene una estimación exacta mediante un número finito de términos.

El valor práctico de las series de Taylor radica en el uso de un número finito de términos que darán una aproximación lo suficientemente cercana a la solución verdadera para propósitos prácticos.

¿Cuántos términos se requieren para obtener una “aproximación razonable”?
La ecuación para el término residual se puede expresar como:
Significa que el error de truncamiento es de orden hn+1. El error es proporcional al tamaño del paso h elevado a la (n+1)-ésima potencia.


Existen series de Taylor para:
  • Función exponencial
  • Logaritmo natural

Serie Geométrica

Teorema del binomio

Funciones trigonométricas:
  • Seno
  • Coseno
  • Tangente
  • Secante
  • Arco seno
  • Arco tangente

Funciones hiperbólicas:
  • Senh
  • Cosh
  • Tanh
  • Senh-1
  • Tanh-1

Aplicaciones

Además de la obvia aplicación de utilizar funciones polinómicas en lugar de funciones de mayor complejidad para analizar el comportamiento local de una función, las series de Taylor tienen muchas otras aplicaciones.
Algunas de ellas son: análisis de límites y estudios paramétricos de los mismos, estimación de números irracionales acotando su error, teorema de L'Hopital para la resolución de límites indeterminados, estudio de puntos estacionarios en funciones (máximos o mínimos relativos o puntos sillas de tendencia estrictamente creciente o decreciente), estimación de integrales, determinación de convergencia y suma de algunas series importantes, estudio de orden y parámetro principal de infinitésimos, etc

http://es.wikipedia.org/wiki/Serie_de_Taylor
http://www.tonahtiu.com/notas/metodos/serie_taylor.htm
Publicado por en No hay comentarios:

miércoles, 25 de mayo de 2011

4.6 Representación de funciones mediante la serie de Taylor.

Definición
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias:
 que puede ser escrito de una manera más compacta como donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.




La función coseno.

Una aproximación de octavo orden de la función coseno en el plano de loscomplejos.

Las dos imágenes de arriba puestas juntas.
A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos dex.

Función exponencial y logaritmo natural

Serie geométrica

\frac{1}{1-x} = \sum^{\infin}_{n=0} x^n\quad\mbox{ para } \left| x \right| < 1


Teorema del binomio

(1+x)^\alpha = \sum^{\infin}_{n=0} \frac{\Gamma(\alpha+1)}{\Gamma(n+1)\Gamma(n-\alpha)} x^n\quad para |x|<1
y cualquier \alpha\quad complejo


Funciones trigonométricas

\sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\quad, \forall x
\cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n}\quad, \forall x
\tan x = \sum^{\infin}_{n=20} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}\quad, \mbox{ para } \left| x \right| < \frac{\pi}{2}
Donde Bs son los Números de Bernoulli.
\sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n}\quad\mbox{, para } \left| x \right| < \frac{\pi}{2}
\csc{x}=\sum_{n=1}^\infty{\frac{2(2^{2n-1}-1)B_{n}x^{2n-1}}{(2n)!}}\quad\mbox{, para } 0<\left |{x}\right |< \pi
\arcsin x = \sum^{\infin}_{n=0} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1
\arctan x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1


Funciones hiperbólicas

\sinh x = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1}\quad , \forall x
\cosh x = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n}\quad , \forall x
\tanh x = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1}\quad\mbox{, para } \left| x \right| < \frac{\pi}{2}
\sinh^{-1} x = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1
\tanh^{-1} x = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1


Función W de Lambert

W_0(x) = \sum^{\infin}_{n=1} \frac{(-n)^{n-1}}{n!} x^n\quad\mbox{, para } \left| x \right| < \frac{1}{e}
Los números Bk que aparecen en los desarrollos de tan(x) y tanh(x) son Números de Bernoulli. Los valores C(α,n) del desarrollo del binomio son los coeficientes binomiales. Los Ek del desarrollo de sec(x) son Números de Euler.


Varias variables

La serie de Taylor se puede generalizar a funciones de d variables:
\sum_{n_1=0}^{\infin} \cdots \sum_{n_d=0}^{\infin} \frac{\partial^{n_1}}{\partial x_1^{n_1}} \cdots \frac{\partial^{n_d}}{\partial x_d^{n_d}} \frac{f(a_1,\cdots,a_d)}{n_1!\cdots n_d!} (x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d} =
\sum_{n=0}^{\infty} {1 \over n!} \sum_{n_1+\cdots+n_d=n} {n \choose n_1 \cdots n_d} {\partial^n f(a_1,\cdots,a_d) \over \partial x_1^{n_1} \cdots \partial x_d^{n_d}} (x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d},
donde {n \choose n_1 \cdots n_d} es
 un coeficiente multinomial.

bibliografia: www.wikipedia.com
Publicado por en No hay comentarios:

jueves, 19 de mayo de 2011

CALCULO DE INTEGRALES DE FUNCIONES EXPRESADAS COMO SERIE DE TAYLOR.

4.7


Sabemos que la recta tangente, como la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia (xo, f(xo)), es aquella recta que pasa por el mencionado punto y tiene la misma pendiente que la curva en ese punto (primera derivada en el punto), lo que hace que la recta tangente y la curva sean prácticamente indistinguibles en las cercanías del punto de tangencia. Gráficamente podemos observar que la curva se pega "suavemente" a la recta en este entorno, de tal manera que "de todas las rectas que pasan por el punto, es esta recta la que más se parece a la curva cerca del punto".


Nótese que cerca del punto de tangencia, la curva se comporta casi linealmente, como se puede apreciar si hacemos acercamientos a la gráfica anterior

Como observamos en los problemas de diferencial, si x se encuentra "lejos" de xo, la recta tangente ya no funciona como aproximador. Parece pues natural preguntarnos por otra función (no lineal) que sirva a nuestros propósitos. La recta tangente es un polinomio de grado 1, el más sencillo tipo de función que podemos encontrar, por lo que podemos tratar de ver si es posible encontrar un polinomio de grado dos que nos sirva para aproximar nuestra función en un rango más grande que la recta tangente.
Veamos que sucede si en lugar de aproximarnos con una recta tratamos de hacerlo con una parábola, es decir tratemos de encontrar de todas las parábolas que pasan por (xo, f(xo)), la que mejor aproxima a la curva, es decir tratemos de encontrar "la parábola tangente" . Nótese que la parábola tangente a una curva no es única.

Naturalmente a esta parábola P(x) = a + b(x- xo) + c(x- xo)2 debemos pedirle que pase por el punto, que tenga la misma inclinación (primera derivada) y la misma concavidad que la parábola (segunda derivada), es decir debemos pedirle:
a)   P(xo) = f (xo)
b)   P ' (xo) = f ' (xo)
c)   P '' (xo) = f '' (xo)
Como P(xo ) = a, P'(x) = b y P''(x) = 2c, concluimos que
a = f (xo),             b = f ' (xo)       y        c = (1/2)f ''(xo)
quedando la ecuación de la parábola que mejor aproxima a la curva en las cercanías de (xo,f(xo)), como:
En la figura de abajo, observamos gráficamente los tres sumandos de la expresión de la parábola tangente. Los dos primeros nos dan la altura sobre la recta tangente y añadiéndole el tercero nos da la altura sobre la parábola tangente.

BILIOGRAFIA
PUEDESOBSERVARMAS SOBRE ESTETEMA EN : http://www.mat.uson.mx/eduardo/calculo2/soltaylor/soltaylorHTML/taylor.htm

Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)