CALCULO DE INTEGRALES DE FUNCIONES EXPRESADAS COMO SERIE DE TAYLOR.

4.7


Sabemos que la recta tangente, como la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia (x_o, f(x_o)), es aquella recta que pasa por el mencionado punto y tiene la misma pendiente que la curva en ese punto (primera derivada en el punto), lo que hace que la recta tangente y la curva sean prácticamente indistinguibles en las cercanías del punto de tangencia. Gráficamente podemos observar que la curva se pega "suavemente" a la recta en este entorno, de tal manera que "de todas las rectas que pasan por el punto, es esta recta la que más se parece a la curva cerca del punto".


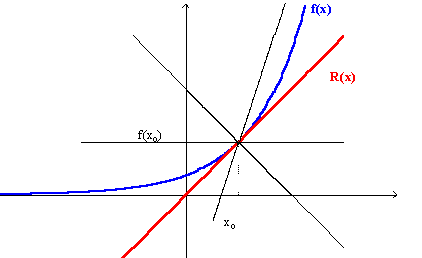
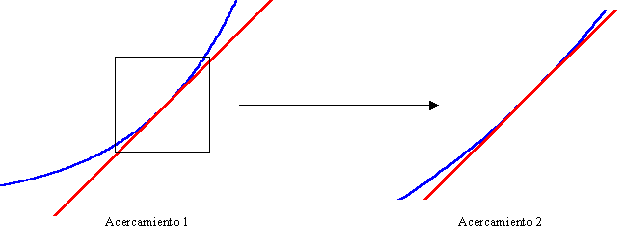
Nótese que cerca del punto de tangencia, la curva se comporta casi linealmente, como se puede apreciar si hacemos acercamientos a la gráfica anterior

Como observamos en los problemas de diferencial, si x se encuentra "lejos" de x_o, la recta tangente ya no funciona como aproximador. Parece pues natural preguntarnos por otra función (no lineal) que sirva a nuestros propósitos. La recta tangente es un polinomio de grado 1, el más sencillo tipo de función que podemos encontrar, por lo que podemos tratar de ver si es posible encontrar un polinomio de grado dos que nos sirva para aproximar nuestra función en un rango más grande que la recta tangente.
Veamos que sucede si en lugar de aproximarnos con una recta tratamos de hacerlo con una parábola, es decir tratemos de encontrar de todas las parábolas que pasan por (x_o, f(x_o)), la que mejor aproxima a la curva, es decir tratemos de encontrar "la parábola tangente" . Nótese que la parábola tangente a una curva no es única.

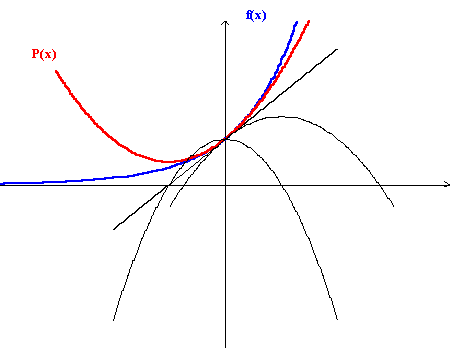
Naturalmente a esta parábola P(x) = a + b(x- x_o) + c(x- x_o)² debemos pedirle que pase por el punto, que tenga la misma inclinación (primera derivada) y la misma concavidad que la parábola (segunda derivada), es decir debemos pedirle:

a)   P(x_o) = f (x_o)
b)   P ' (x_o) = f ' (x_o)
c)   P '' (x_o) = f '' (x_o)

Como P(x_o ) = a, P'(x) = b y P''(x) = 2c, concluimos que

a = f (x_o),             b = f ' (x_o)       y        c = (1/2)f ''(x_o)

quedando la ecuación de la parábola que mejor aproxima a la curva en las cercanías de (x_o,f(x_o)), como:

En la figura de abajo, observamos gráficamente los tres sumandos de la expresión de la parábola tangente. Los dos primeros nos dan la altura sobre la recta tangente y añadiéndole el tercero nos da la altura sobre la parábola tangente.

BILIOGRAFIA
PUEDESOBSERVARMAS SOBRE ESTETEMA EN : http://www.mat.uson.mx/eduardo/calculo2/soltaylor/soltaylorHTML/taylor.htm