SERIE NUMERICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (criterio de D´Alembert) y PRUEBA DE LA RAÍZ (criterio de Cauchy).
Imaginemos que se va a celebrar una carrera con las siguientes reglas:
1. El primer minuto debe recorrerse 100 metros.
2. El minuto siguiente debe recorrerse la mitad, 50 metros.
3. El minuto siguiente debe recorrerse la mitad del anterior, 25 metros.
4. El minuto siguiente dee recorrerse la mitad del anterior, 12,50 metros.
y as´ı sucesivamente.
Por otra parte, al mismo tiempo empieza otra carrera, con las reglas ligeramente
modificadas:
1. El primer minuto se recorren 100 metros.
2. El minuto siguiente se recorren la mitad de 100 metros, 50 metros.
3. El minuto siguiente se recorren la tercera parte de 100 metros, 33,3
metros.
4. El minuto siguiente se recorren la cuarta parte de 100 metros, 25 metros.
y as´ı sucesivamente.
Dos corredores empiezan a la vez las carreras. Si la meta de la primera se
encuentra situada a 300 metros y la de la segunda a 1000 metros, ¿qui´en
llega primero a la meta y cu´anto tiempo tarda?
Llamamos D = 100 metros la distancia recorrida en el primer minuto. La
primera carrera va recorriendo las distancias:
D +D/2+D/4+D/8+ . . .
La segunda carrera va recorriendo las distancias:
D +D/2+D/3+D/4+ . . .
La pregunta es cu´al de estas sumas alcanza la distancia a la que est´a situada
la meta respectiva. Al acabar este tema deberemos ser capaces de dar una
respuesta razonada1.
Series de Convergencia
Son aplicables en caso de disponer de otra serie tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:

CONVERGENCIA
Criterio de D'Alembert
Criterio de Cauchy
 converge
converge
Imaginemos que se va a celebrar una carrera con las siguientes reglas:
1. El primer minuto debe recorrerse 100 metros.
2. El minuto siguiente debe recorrerse la mitad, 50 metros.
3. El minuto siguiente debe recorrerse la mitad del anterior, 25 metros.
4. El minuto siguiente dee recorrerse la mitad del anterior, 12,50 metros.
y as´ı sucesivamente.
Por otra parte, al mismo tiempo empieza otra carrera, con las reglas ligeramente
modificadas:
1. El primer minuto se recorren 100 metros.
2. El minuto siguiente se recorren la mitad de 100 metros, 50 metros.
3. El minuto siguiente se recorren la tercera parte de 100 metros, 33,3
metros.
4. El minuto siguiente se recorren la cuarta parte de 100 metros, 25 metros.
y as´ı sucesivamente.
Dos corredores empiezan a la vez las carreras. Si la meta de la primera se
encuentra situada a 300 metros y la de la segunda a 1000 metros, ¿qui´en
llega primero a la meta y cu´anto tiempo tarda?
Llamamos D = 100 metros la distancia recorrida en el primer minuto. La
primera carrera va recorriendo las distancias:
D +D/2+D/4+D/8+ . . .
La segunda carrera va recorriendo las distancias:
D +D/2+D/3+D/4+ . . .
La pregunta es cu´al de estas sumas alcanza la distancia a la que est´a situada
la meta respectiva. Al acabar este tema deberemos ser capaces de dar una
respuesta razonada1.
Series de Convergencia
Son aplicables en caso de disponer de otra serie
 tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
Criterio de comparación directa ( de la mayorante o de Gauss )
Si 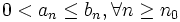
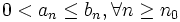
- Si
 converge
converge  converge
converge - Si
 diverge
diverge  diverge
diverge
Criterio de comparación por paso al límite del cociente

Entonces:
- Si L = 0 y
 converge
converge  converge
converge - Si
 y
y  diverge
diverge  diverge
diverge - En otro caso, ambas series comparten la misma condición (ambas convergen, o bien ambas son divergentes).
CONVERGENCIA
Una serie alternada an converge absolutamente si

es una serie convergente. Se demuestra que una serie que converge absolutamente, es una serie convergente.
Criterio de D'Alembert
Sea una serie  , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).
 , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).Si existe
con 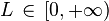 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:
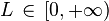 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:- si L < 1, la serie converge.
- si L > 1, entonces la serie diverge.
- si L = 1, no es posible decir algo sobre el comportamiento de la serie.
En este caso, es necesario probar otro criterio, como el criterio de Raabe
Criterio de Cauchy
Si f(x) es una función positiva y monótonamente decreciente definida en el intervalo [1, ∞) tal que f(n) = an para todo n, entonces  converge si y sólo si
converge si y sólo si  es finita.
es finita.
 converge si y sólo si
converge si y sólo si  es finita.
es finita.Más generalmente, y para el tipo de función definida antes, pero en un intervalo [N,∞), la serie
converge si y sólo si la integral
converge
 converge
convergeBIBLIOGRAFIA:
http://es.wikipedia.org/wiki/Serie_matemática#Criterio_de_D.27Alembert_o_Criterio_del_Cociente_.28Criterio_de_la_raz.C3.B3n.29
MC. Marcel Ruiz Martínez
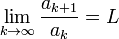
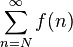
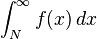
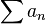 una serie monótona de números positivos decrecientes.
una serie monótona de números positivos decrecientes.  converge si y sólo si la serie
converge si y sólo si la serie
No hay comentarios:
Publicar un comentario