En matemáticas, una serie es la suma de los términos de una sucesión.
Se representa una serie con términos an como
Siendo N es el índice final de la serie.
Siendo N es el índice final de la serie.
Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales.
Las series convergen o divergen.
Una serie diverge si
No existe o si tiende a infinito;
Converge si:
Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir, .
Las series convergen o divergen. En cálculo, una serie diverge si no existe o si tiende a infinito; puede converger si para algún .
Serie finita
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de Cauchy de y se verifica es . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
Serie infinita
Primer ejemplo. Para alguna , sea y . Entonces
Las series convergen o divergen. En cálculo, una serie diverge si no existe o si tiende a infinito; puede converger si para algún .
Serie finita
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de Cauchy de y se verifica es . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
Serie infinita
Primer ejemplo. Para alguna , sea y . Entonces
por definición y la fórmula binomial. Dado que, formalmente, y , se ha demostrado que . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series (véase debajo), se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo .
Segundo ejemplo. Sea x(n) = 1 para todo . Entonces C(x,x)(n) = n + 1 para todo por lo tanto el producto de Cauchy y no es convergente.
 tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces: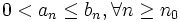
 converge
converge diverge
diverge  diverge
diverge
 converge
converge  converge
converge y
y 
 , tal que
, tal que 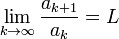
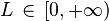 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que: converge si y sólo si
converge si y sólo si  es finita.
es finita.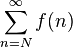
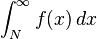
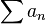 una serie monótona de números positivos decrecientes.
una serie monótona de números positivos decrecientes.  converge si y sólo si la serie
converge si y sólo si la serie converge
converge

 complejo
complejo es
es